
ピボットテーブルやピボットグラフを使う取っ掛かりとして、ゆるく読んでいただけたら嬉しいです!
株に詳しいわけじゃないけど、Power Query(パワークエリ)で整えた株価指数データを準備して…
ちょっと遊んでみよう!というノリで、いろいろグラフにしてみました。
本格的な投資分析ではありません。大したことはできませんので、そこはご容赦ください。
目的は、ピボットテーブルやピボットグラフで「こうやって見えるんだ〜」という体験をしてもらうことです。
- 本記事で使用しているデータは、あくまでピボットテーブル、ピボットグラフ、Power QueryなどのExcelの機能を紹介するためのものであり、内容の正確性や整合性を確認したものではありません。
- データはサンプルとして取り扱っており、実際の株価や市場データとは異なる場合があります。
- 本記事の内容をもとに、株式売買などの投資判断を行うことは推奨しておりません。
- 株式取引はリスクを伴う行為であり、最終的な判断はすべてご自身の責任でお願いいたします。
- データの活用については、目的に応じて適切な確認・加工を行った上で使用してください。
まずは準備!加工済みの株価データを読み込み
今回は、実際の株価指数データを使っていきます。
指数はS&P500、期間は1990年~2025年3月までを使います。
Excelにテーブルとして読み込んで、Power Queryや関数を使って「前年差」「年リターン(前年比)」「対数」などを計算しました。
年リターンはシンプルに「(年末の終値 ÷ 前年末の終値)-1」で求めます。
対数は常用対数を取っています。
あくまで素人の計算なので、正確じゃないかもしれません。
グラフはメニューの「挿入」→「ピボットグラフ」をクリックして、あとはグラフの種類を選べばOKです!
ピボットグラフでできないグラフは「挿入」からグラフの種類を選んで作ります。
今回は、グラフの見た目にはあまりこだわらず、サクッと作っていきますね。
ピボットテーブルでは「集計フィールド」を使えば、新しい項目を作って、自分で数式を入力することができます。
メニューの「ピボットテーブル分析」→「フィールド/アイテム/セット」→「集計フィールド」で表示される「集計フィールドの挿入」ダイアログで新規フィールドを作ります。
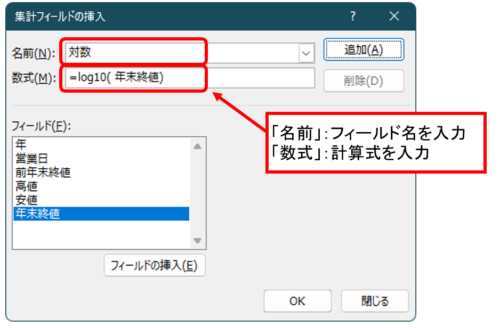
しかし、「Excel で計算フィールドの総計の値が正しくない」という問題があります。
計算ミスがあるといけないので今回は使わないことにします。
ゆるっと分析タイム
まずは年別データを使います。
とりあえずグラフにしてみる!ざっくり株価の動きをチェック
まずはシンプルに、「年末の終値」を折れ線グラフにしてみます。
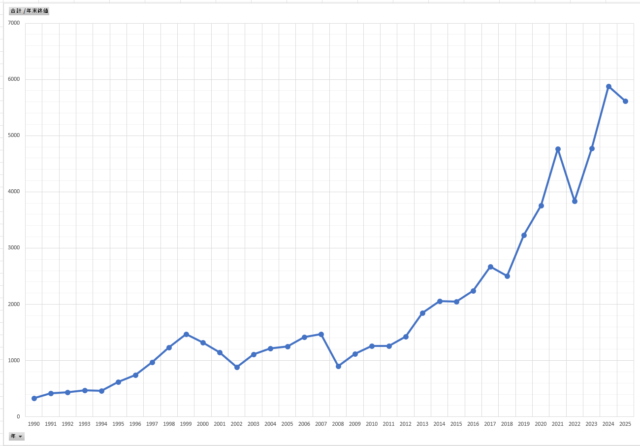
よくあるやつですね。これにその年の「高値」「安値」を追加します。
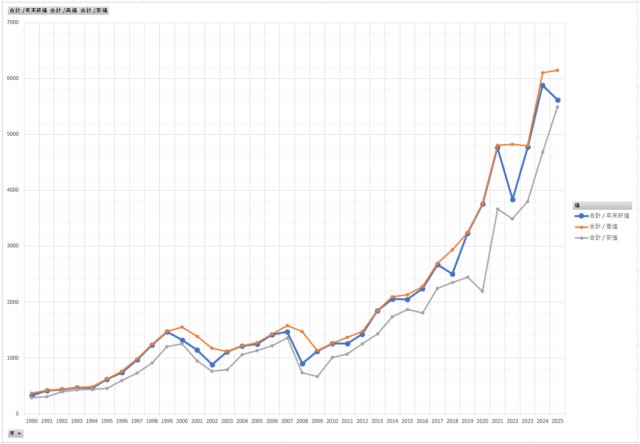
青が「年末終値」、オレンジが「年高値」、グレーが「年安値」です。
やっぱり株価を見るならローソク足ですよね!というわけで、ローソク足でも表示してみます。
Excelでもちゃんとローソク足グラフが作れるんです。
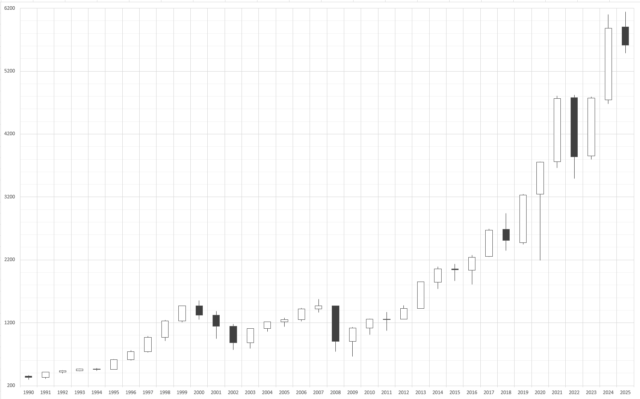
対数スケールで見ると、印象が変わる!?
通常グラフと対数グラフを比較してみます。
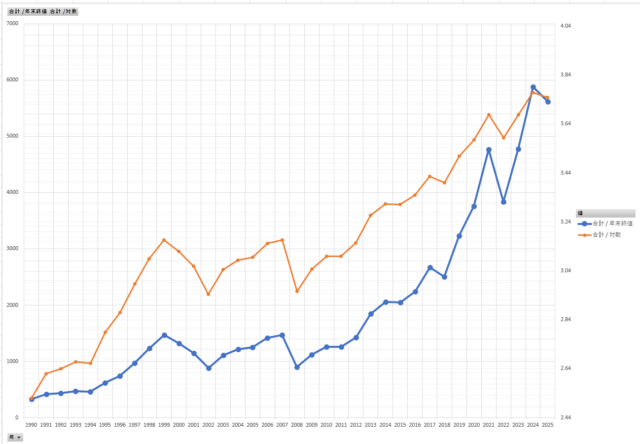
青が「株価」、オレンジが「対数スケール」になっています。
スタートとゴールの位置がほぼ合うように縦軸をいじっています。
対数グラフは直線的に変化していると聞くので、参考に直線を引いてみました。ただ図形ツールで線を引いただけです。
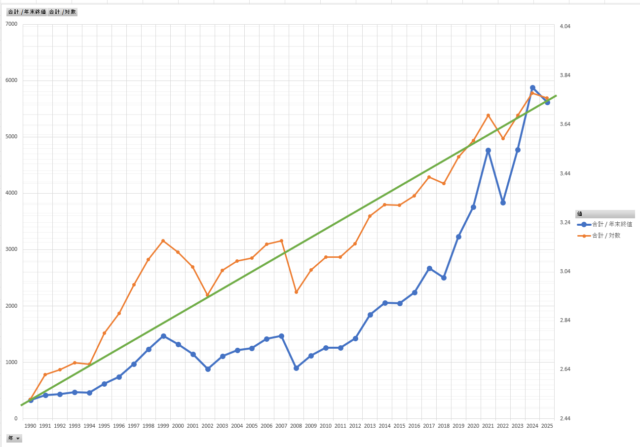
対数スケールで見ると、1990年代の伸び方がかなり目立ちますね〜。
ふと気になったので、「年末終値」「年高値」「年安値」をすべて対数で表します。
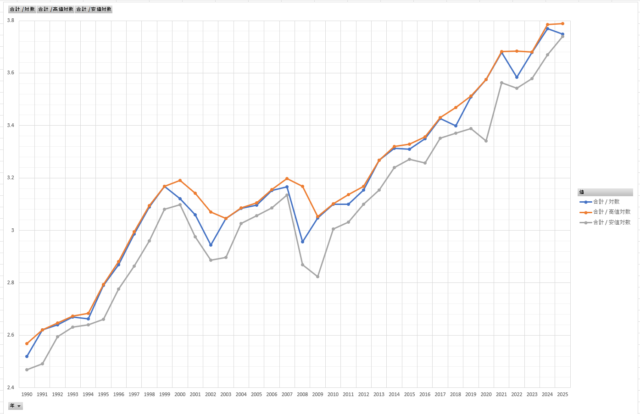
青が「年末終値」、オレンジが「年高値」、グレーが「年安値」です。
株価のグラフに比べると、前半部分の差がめちゃ分かりやすい!
対数スケールでもローソク足で表示してみましょう!
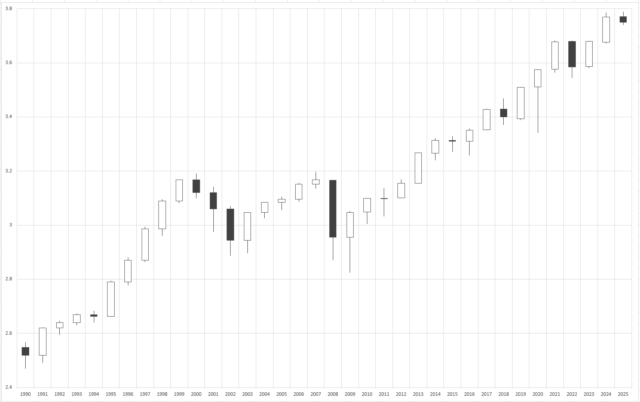
年ごとのリターンをグラフ化する
「株価」のグラフに「年リターン」を重ねて表示してみます。
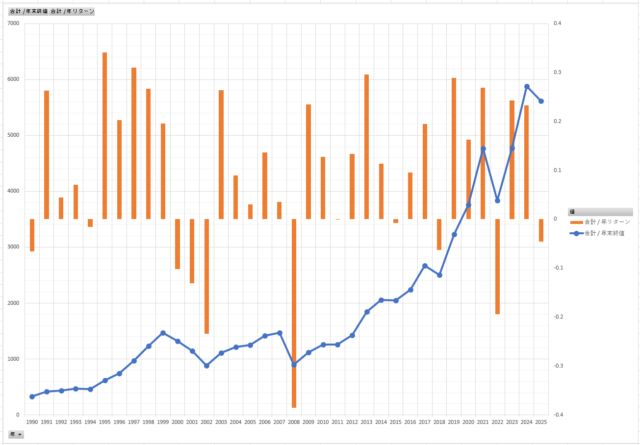
株価の折れ線グラフは「年末の終値」を使っているので、スタートの1990年がマイナスだったことに気づきにくいですね。
折れ線グラフだけ見ると1990年から1999年までずっと上昇していると錯覚します。
次に、「対数」のグラフに「年リターン」を重ねて表示してみます。
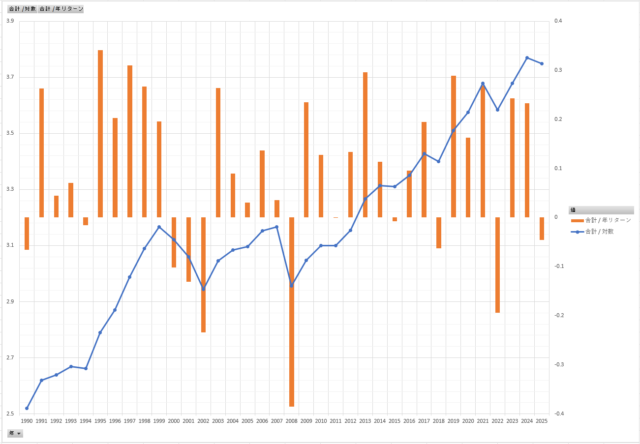
こちらの方が折れ線グラフの増減と、年リターンの棒グラフがリンクした感じがします。
1994年から1999年にかけての上昇がすごい!
そして、2008年のマイナスがきつい!2000年~2002年の3年連続のマイナスもかなりきつい。
見てるだけで震えます…
年平均リターンとリスクを計算する
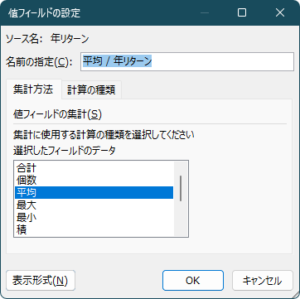
年平均リターンを計算します。
ちょっと調べてみたところ、「算術平均リターン」と「幾何平均リターン」の2種類があるみたいなので、両方計算してみることにします。
以下の計算式で計算しました。
- 算術平均
各年の年リターン / 年数 - 幾何平均
{ ( 期間の最後の終値 / 期間の最初の前日終値 ) ^ ( 1 / 年数 ) } – 1
算術平均リターンはピボットテーブルでサクッと平均を出せますが、幾何平均リターンの方は「期間の最初と最後の終値」を使うので、Excelの関数で計算してもらうことにしました。
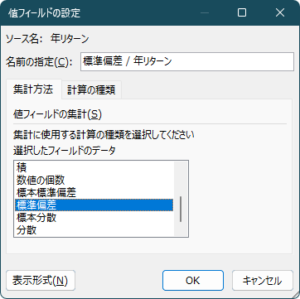
リスクは「標準偏差」らしいので、ピボットテーブルの「値フィールドの設定」で集計方法を「標準偏差」にして計算します。
結果がこちら。気になったところを切り取って計算しています。
| 期間 | 年数 | 算術平均リターン | 幾何平均リターン | リスク |
|---|---|---|---|---|
| 1990年~2024年 | 35年 | 9.84% | 8.37% | 16.96% |
| 1991年~1999年 | 9年 | 18.65% | 18.04% | 11.84% |
| 2000年~2002年 | 3年 | -15.52% | -15.71% | 5.68% |
| 2008年(参考) | 1年 | -38.49% | ||
| 2009年~2024年 | 16年 | 13.30% | 12.42% | 13.48% |
| 2020年~2024年 | 5年 | 14.25% | 12.73% | 17.21% |
一部手作業で処理しているので、もし間違っていたらごめんなさい…!
また、端数処理もあまり気にせず計算しているので、多少の誤差は出てくるかもと思います。
だいたいの目安ぐらいに思ってください。
単純に数字の差だけ見れば、算術平均リターンと幾何平均リターンにあまり差はないんですね。もっと差が出ると思ってました。
1990年代のプラスと、2000〜2002年&2008年のマイナスっぷりはインパクトありますね〜。
1990年からの35年間で平均リターン約8%って十分すごい数字だと思うけれど、ここ数年は約12%。これはかなりすごいですよね。
日別データをグラフでチェック!
ここからは日別データを使っていきます。
株価の「前日比」を、日ごとに棒グラフで見ていきます。
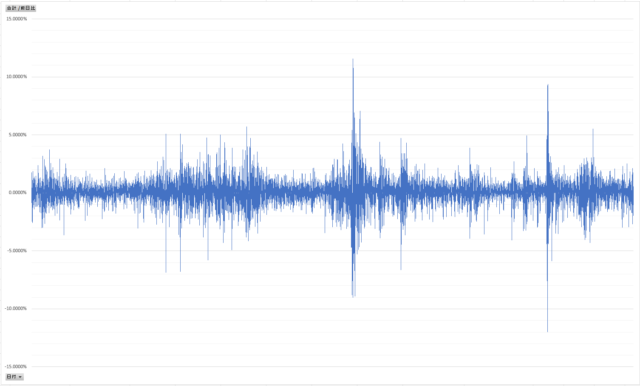
上にも下にも大きく動くタイミングは、だいたい同じことが多い――そんな話、よく聞きますよね。
「前日比」がどんなふうに分布しているかも見てみましょう。
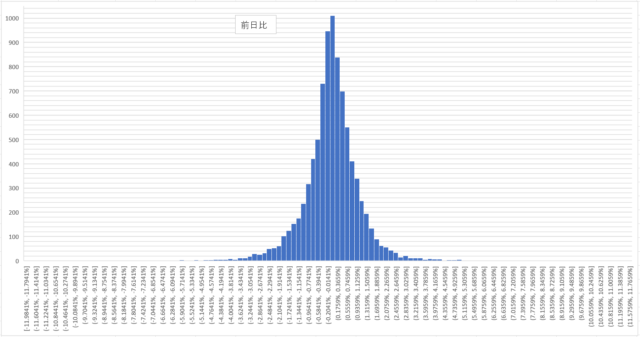
これは…正規分布っぽい形になってるでしょうか。
曜日ごとの傾向は?
まずは、曜日ごとの「プラス・マイナスの回数」「前日比の平均」「標準偏差」を見てみましょう。
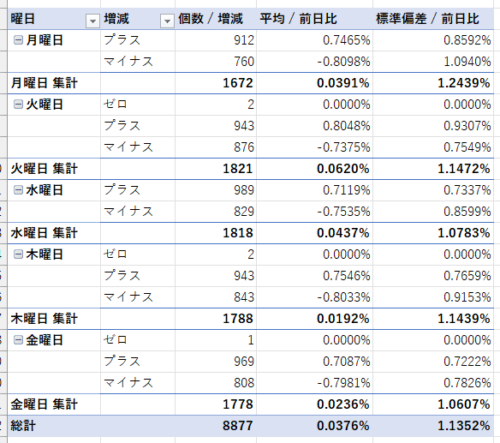
「プラス」は前日比で株価が上がった日のことです。「マイナス」はその逆で、下がった日ですね。
曜日による差はあまりなさそうですが、「前日比の平均」と「標準偏差」をグラフにしてみます。
青の棒グラフが「前日比の平均」、オレンジの折れ線グラフが「前日比の標準偏差」です
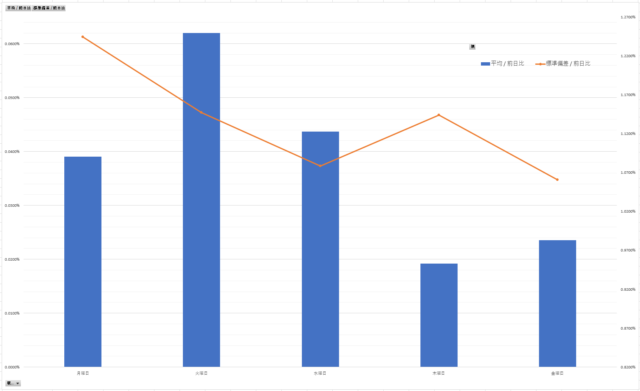
グラフはデコボコしていますが、数字の差は小さくて「これって誤差じゃないの?」と思うくらい。
投資の世界ではこういう微妙な差も何か意味があるのか…どうなんでしょうね。
実際、曜日で投資判断を変える人は、あまりいないかもしれませんね。
月別に見てみよう
月ごとの「プラス・マイナスの回数」「前日比の平均」「標準偏差」をチェックすると──
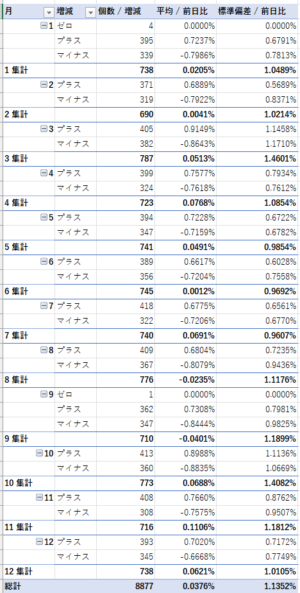
月ごとの「前日比の平均」と「前日比の標準偏差」をグラフにします。
青の棒グラフが「前日比の平均」、オレンジの折れ線グラフが「前日比の標準偏差」です。
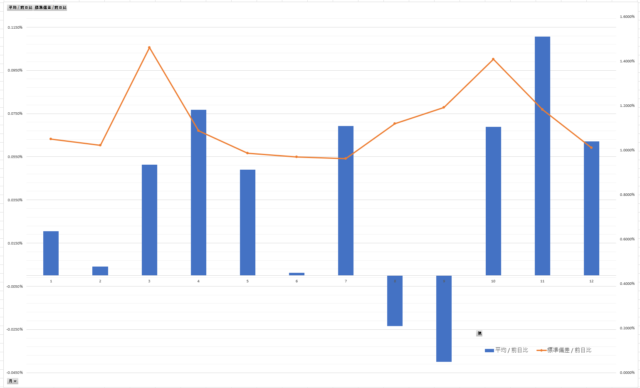
8月と9月は平均がマイナス傾向。ちょっと元気がない感じ。
逆に、3月~5月、それから10月~12月あたりは上昇しやすい時期みたいです。
日別(1日~31日)の場合は?
日ごと(1日~31日単位)の「前日比の平均」と「前日比の標準偏差」をグラフ化。
青の棒グラフが「前日比の平均」、オレンジの折れ線グラフが「前日比の標準偏差」です。
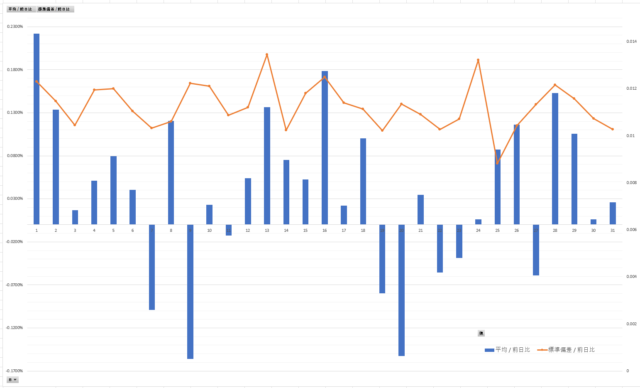
平均がマイナスとなっている日がチラホラとありますね。
まとめ
今回は、株価指数データを使って、Power Queryでのデータ加工、ピボットテーブルでの集計、ピボットグラフでの可視化と、Excelの便利な機能をいろいろ活用してみました。
難しい関数や複雑な数式を使わなくても、機能をうまく組み合わせるだけで、柔軟にデータを扱えるのがExcelの魅力ですね。
Power Queryで整えたデータを、ピボットテーブルで自在に動かせるのは便利です。
今回はあくまでも「分析ごっこ」的な内容ではありましたが、こうした機能を使ってちょっとしたデータの観察やグラフ作成を気軽に楽しめることが伝わればうれしいです。

Excelの機能の面白さ、少しでも感じてもらえたでしょうか?



